若有穷数列 (
( 是正整数),满足
是正整数),满足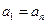 ,
, ,
, ,
,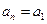 ,即
,即 (
( 是正整数,且
是正整数,且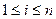 ),就称该数列为“对称数列”.
),就称该数列为“对称数列”.
(1)已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且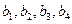 成等差数列,
成等差数列, ,试写出
,试写出 的每一项.
的每一项.
(2)已知 是项数为
是项数为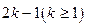 的对称数列,且
的对称数列,且 构成首项为50,公差为
构成首项为50,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为 ,则当
,则当 为何值时,
为何值时, 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的对称数列,使得
的对称数列,使得 成为数列中的连续项;当
成为数列中的连续项;当 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和 .
.
推荐套卷
若有穷数列 (
( 是正整数),满足
是正整数),满足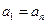 ,
, ,
, ,
,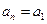 ,即
,即 (
( 是正整数,且
是正整数,且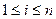 ),就称该数列为“对称数列”.
),就称该数列为“对称数列”.
(1)已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且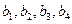 成等差数列,
成等差数列, ,试写出
,试写出 的每一项.
的每一项.
(2)已知 是项数为
是项数为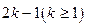 的对称数列,且
的对称数列,且 构成首项为50,公差为
构成首项为50,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为 ,则当
,则当 为何值时,
为何值时, 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的对称数列,使得
的对称数列,使得 成为数列中的连续项;当
成为数列中的连续项;当 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和 .
.