（本小题满分12分）
已知函数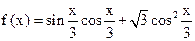
．
（I）将函数f(x)写成f(x)=
（
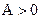）的形式，并求其图像对称中心的横坐标；
（Ⅱ）如果△ABC的三边a、b、c所对的角分别为A ,B ,C且满足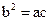
，且边b所对的角为B，试求角B的取值范围及此时函数f(B)的值域.
相关试题
表示两条直线,求m的值
过点(1,2)和第一,二,四象限,若相关知识点
推荐套卷
（本小题满分12分）
已知函数．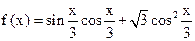
（I）将函数f(x)写成f(x)=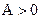（）的形式，并求其图像对称中心的横坐标；
（Ⅱ）如果△ABC的三边a、b、c所对的角分别为A ,B ,C且满足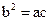，且边b所对的角为B，试求角B的取值范围及此时函数f(B)的值域.
粤公网安备 44130202000953号