(本题满分16分,第1小题5分,第2小题6分,第3小题5分)
已知函数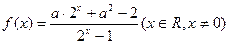 ,其中
,其中 为常数,且
为常数,且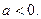
(1)若 是奇函数,求
是奇函数,求 的取值集合A;
的取值集合A;
(2)(理)当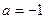 时,设
时,设 的反函数为
的反函数为 ,且函数
,且函数 的图像与
的图像与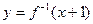 的图像关于
的图像关于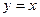 对称,求
对称,求 的取值集合B;
的取值集合B;
(文)当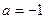 时,求
时,求 的反函数;
的反函数;
(3)(理)对于问题(1)(2)中的A、B,当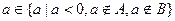
 时,不等式
时,不等式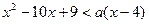 恒成立,求
恒成立,求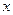 的取值范围。
的取值范围。
(文)对于问题(1)中的A,当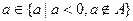 时,不等式
时,不等式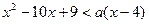 恒成立,求
恒成立,求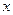 的取值范围。
的取值范围。
相关知识点
推荐套卷
(本题满分16分,第1小题5分,第2小题6分,第3小题5分)
已知函数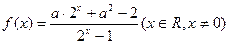 ,其中
,其中 为常数,且
为常数,且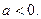
(1)若 是奇函数,求
是奇函数,求 的取值集合A;
的取值集合A;
(2)(理)当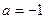 时,设
时,设 的反函数为
的反函数为 ,且函数
,且函数 的图像与
的图像与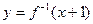 的图像关于
的图像关于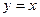 对称,求
对称,求 的取值集合B;
的取值集合B;
(文)当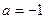 时,求
时,求 的反函数;
的反函数;
(3)(理)对于问题(1)(2)中的A、B,当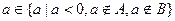
 时,不等式
时,不等式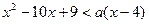 恒成立,求
恒成立,求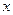 的取值范围。
的取值范围。
(文)对于问题(1)中的A,当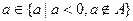 时,不等式
时,不等式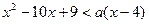 恒成立,求
恒成立,求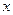 的取值范围。
的取值范围。