设{an}是正数组成的数列，其前n项和为Sn，并且对于所有的n
N+，都有
。
（1）写出数列{an}的前3项；
（2）求数列{an}的通项公式(写出推证过程)；
（3）设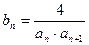
，
是数列{bn}的前n项和，求使得
对所有nN+都成立的最小正整数
的值。
相关试题
分别为∠A、∠B、∠C所对的边，且
，求△ABC周长的取值范围．
的前四项的和为
，且
成等比数列．
与前n项和
；
为数列
的前n项和，求
实数
满足
,命题
实数
，若
是
的充分不必要条件,求实数
的取值范围.
的不等式
的解集为
.
的值；
（
为常数）.
的内角
所对边分别为
，且
.
的大小；
，求边长
的最小值．推荐套卷
设{an}是正数组成的数列，其前n项和为Sn，并且对于所有的nN+，都有。
（1）写出数列{an}的前3项；
（2）求数列{an}的通项公式(写出推证过程)；
（3）设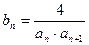，是数列{bn}的前n项和，求使得对所有nN+都成立的最小正整数的值。
粤公网安备 44130202000953号