设
分别是椭圆C：
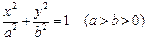的左右焦点，
（1）设椭圆C上的点
到两点距离之和等于4，写出椭圆C的方程和焦点坐标。
（2）设K是（1）中所得椭圆上的动点，求线段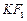
的中点B的轨迹方程。
（3
）设点P是椭圆C 上的任意一点，过原点的直线L与椭圆相交于M，N两点，当直线PM ，PN的斜率都存在，并记为
试探究
的值是否与点P及直线L有关，并证明你的结论。
，
满足
。求函数
在
上的最大值和最小值。
为锐角，且
。
的值。
的值。
，
，
，
，求
的值。
， 求
的值。
中，
，弧
的长为
，求此扇形内切圆的面积。
推荐套卷
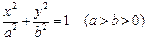设分别是椭圆C：的左右焦点，
（1）设椭圆C上的点到两点距离之和等于4，写出椭圆C的方程和焦点坐标。
（2）设K是（1）中所得椭圆上的动点，求线段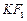的中点B的轨迹方程。
（3）设点P是椭圆C 上的任意一点，过原点的直线L与椭圆相交于M，N两点，当直线PM ，PN的斜率都存在，并记为 试探究的值是否与点P及直线L有关，并证明你的结论。
粤公网安备 44130202000953号