2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽
的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形
拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的
面积为25,直角三角形中较小的锐角为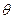 ,那么
,那么 的值等于 .
的值等于 .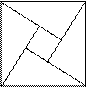
推荐套卷
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽
的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形
拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的
面积为25,直角三角形中较小的锐角为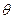 ,那么
,那么 的值等于 .
的值等于 .