 直角三角形
直角三角形 的直角顶点
的直角顶点 为动点,
为动点, ,
,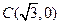 为两个定点,作
为两个定点,作 于
于 ,动点
,动点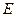 满足
满足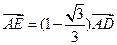 ,当点
,当点 运动时,设点
运动时,设点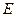 的轨迹为曲线
的轨迹为曲线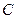 ,曲线
,曲线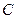 与
与 轴正半轴的交点为
轴正半轴的交点为 .
.
(Ⅰ) 求曲线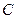 的方程;
的方程;
(Ⅱ) 是否存在方向向量为m 的直线
的直线 ,与曲线
,与曲线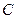 交于
交于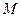 ,
,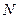 两点,且
两点,且 与
与 的夹角为
的夹角为 ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
推荐套卷
 直角三角形
直角三角形 的直角顶点
的直角顶点 为动点,
为动点, ,
,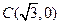 为两个定点,作
为两个定点,作 于
于 ,动点
,动点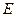 满足
满足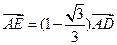 ,当点
,当点 运动时,设点
运动时,设点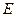 的轨迹为曲线
的轨迹为曲线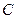 ,曲线
,曲线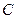 与
与 轴正半轴的交点为
轴正半轴的交点为 .
.
(Ⅰ) 求曲线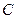 的方程;
的方程;
(Ⅱ) 是否存在方向向量为m 的直线
的直线 ,与曲线
,与曲线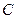 交于
交于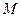 ,
,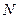 两点,且
两点,且 与
与 的夹角为
的夹角为 ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.