如图,椭圆的中心在原点,
为椭圆的左焦点, 
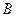为椭圆的一个顶点,过点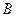作与
垂直的直线
交
轴于
点, 且椭圆的长半轴长
和短半轴长
是关于的方程
(其中
为半焦距)的两个根.
(1)求椭圆的离心率;
(2)经过、、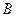三点的圆与直线
相切，试求椭圆的方程.
相关试题
km处的海岸渔站中，如果送信人步行每小时5km，船速每小时4km，问应在何处登岸可以使抵达渔站的时间最省？
．
过抛物线
的焦点，并且与抛物线相交于
和
两点
.求证：对于此抛物线的任意给定的一条弦
，直线
，求证：
．推荐套卷
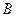如图,椭圆的中心在原点,为椭圆的左焦点, 为椭圆的一个顶点,过点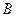作与垂直的直线交轴于点, 且椭圆的长半轴长和短半轴长是关于的方程(其中为半焦距)的两个根.
(1)求椭圆的离心率;
(2)经过、、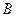三点的圆与直线相切，试求椭圆的方程.
粤公网安备 44130202000953号