某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本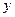
（万元）与年产量
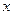（吨）之间的函数关系式可以近似地表示为
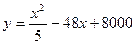，已知此生产线年产量最大为210吨。
（1）求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；
（2）若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？
相关试题
，求函数
的最大值和最小值；
中，底面
为正方形，
平面
，点
是
的中点．
//平面
；
的体积为
，求
的长．
.
的最小正周期； 
时,求函数
的值；
,
,求数列
的前
项和
；推荐套卷
某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本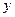（万元）与年产量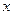（吨）之间的函数关系式可以近似地表示为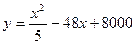，已知此生产线年产量最大为210吨。
（1）求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；
（2）若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？
粤公网安备 44130202000953号