(本小题满分12分)
已知函数
的图象过坐标原点O,且在点
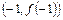处的切线的斜率是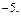
（1）求实数
的值；
（2）求
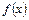在区间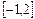
上的最大值；
（3）对任意给定的正实数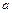
，曲线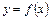
上是否存在两点P、Q，使得
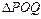是以O为直角顶点的直角三角形，且此三角形斜边中点在
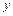轴上？说明理由。
，求f（
）的值.
－α）=－cosα；
，cos（α+β）=1，求证：cos（2α+β）=
．推荐套卷
(本小题满分12分)
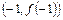已知函数的图象过坐标原点O,且在点处的切线的斜率是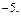
（1）求实数的值；
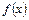（2）求在区间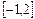上的最大值；
（3）对任意给定的正实数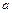，曲线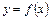上是否存在两点P、Q，使得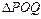是以O为直角顶点的直角三角形，且此三角形斜边中点在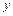轴上？说明理由。
粤公网安备 44130202000953号