（本小题满分14分）
某厂生产
某种产品的年固定成本为250万元，每生产
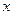千件，需另投入成本为
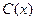，当年产量不足
80千件时，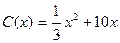
（万元）；当年产量不小于80千件时，
（万元），通过市场分析，若每件售价为500元时，该厂当年生产该产品能全部销售完。
（1）写出年利润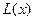
（万元）关于年产量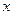（千件）的函数解析式；
（2）年产量为多少千件时，该厂在这一产品的生产中所获利润最大，最大利润是多少？
相关试题
。
的定义域；
的值，作出函数
的图象并指出函数
,
,
。
,
；
,求实数
的取值范围.
，
.
，若
，求
的值；
，当
时，求
在
上的最小值；
在区间
上的最大值.
，
是定义域为
的奇函数．
的值，判断并证明当
时，函数
，函数
，求
的值域；
，若
对于
时恒成立.请求出最大的整数
．
是定义域为R的奇函数.当
时，
，图像如图所示.
有两解，写出
的范围；
，写出解集.推荐套卷
（本小题满分14分）
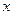某厂生产某种产品的年固定成本为250万元，每生产千件，需另投入成本为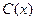，当年产量不足80千件时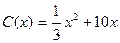，（万元）；当年产量不小于80千件时，（万元），通过市场分析，若每件售价为500元时，该厂当年生产该产品能全部销售完。
（1）写出年利润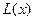（万元）关于年产量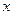（千件）的函数解析式；
（2）年产量为多少千件时，该厂在这一产品的生产中所获利润最大，最大利润是多少？
粤公网安备 44130202000953号