（本小题满分14分）已知函数
.
（1）证明：函数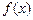
对于定义域内任意
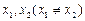都有：
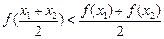成立.
（2）已知
的三个顶点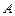
、
、
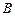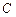都在函数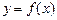
的图象上，且横坐标依次成等差数列，求证：是钝角三角形，但不可能是等腰三角形.
相关试题
为定义在
上的奇函数，当
时，
；
上的单调性，并给出证明.
，
的定义域为R，求实数
的取值范围.
的单调递减区间（—∞,2],求函数
的最大值.
在(－∞，0)上的增减性．
，
在
处与直线
相切；
的值；②求函数
上的最大值;
时，若不等式
对所有的
都成立，求实数
的取值范围.相关知识点
推荐套卷
（本小题满分14分）已知函数.
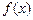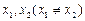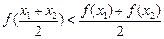（1）证明：函数 对于定义域内任意都有：成立.
（2）已知的三个顶点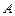、、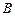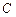都在函数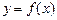的图象上，且横坐标依次成等差数列，求证：是钝角三角形，但不可能是等腰三角形.
粤公网安备 44130202000953号