(本小题满分14分)已知椭圆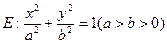 的左、右焦点分别为
的左、右焦点分别为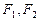 ,点
,点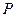 是
是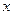 轴上方椭圆
轴上方椭圆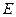 上的一点,且
上的一点,且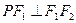 ,
,  ,
, 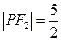 .
.
(Ⅰ)求椭圆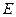 的方程和
的方程和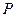 点的坐标;
点的坐标;
(Ⅱ)判断以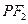 为直径的圆与以椭圆
为直径的圆与以椭圆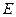 的长轴为直径的圆的位置关系;
的长轴为直径的圆的位置关系;
(Ⅲ)若点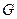 是椭圆
是椭圆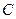 :
: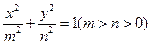 上的任意一点,
上的任意一点, 是椭圆
是椭圆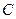 的一个焦点,探究以
的一个焦点,探究以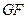 为直径的圆与以椭圆
为直径的圆与以椭圆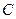 的长轴为直径的圆的位置关系.
的长轴为直径的圆的位置关系.
推荐套卷
(本小题满分14分)已知椭圆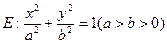 的左、右焦点分别为
的左、右焦点分别为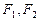 ,点
,点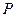 是
是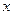 轴上方椭圆
轴上方椭圆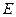 上的一点,且
上的一点,且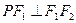 ,
,  ,
, 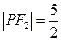 .
.
(Ⅰ)求椭圆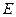 的方程和
的方程和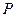 点的坐标;
点的坐标;
(Ⅱ)判断以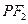 为直径的圆与以椭圆
为直径的圆与以椭圆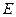 的长轴为直径的圆的位置关系;
的长轴为直径的圆的位置关系;
(Ⅲ)若点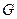 是椭圆
是椭圆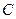 :
: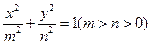 上的任意一点,
上的任意一点, 是椭圆
是椭圆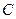 的一个焦点,探究以
的一个焦点,探究以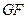 为直径的圆与以椭圆
为直径的圆与以椭圆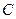 的长轴为直径的圆的位置关系.
的长轴为直径的圆的位置关系.