(本小题满分12分)
某同学 参加3门课程的考试.假
参加3门课程的考试.假 设该同学第一门课程取得优秀成绩的概率为
设该同学第一门课程取得优秀成绩的概率为 ,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
| ξ |
0 |
1 |
2 |
3 |
| p |
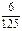 |
a |
b |
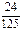 |
(I)求该生至少有1门课程取得优秀成绩的概率;
(II)求p,q的值;
(III)求数学期望Eξ.
相关知识点
推荐套卷
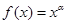 过点(2,4),求出
过点(2,4),求出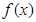 的解析式并用单调性定义证明
的解析式并用单调性定义证明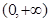 上为增函数。
上为增函数。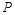 、
、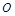 分别是正四棱柱
分别是正四棱柱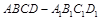 上、下底面的中
上、下底面的中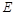 是
是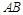 的中点,
的中点,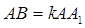 .
.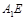 ∥平面
∥平面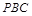 ;
;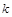 取何值时,
取何值时,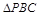 的重心?
的重心?
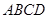 中,
中,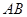 ∥
∥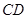 ,
,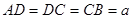 ,
,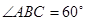 ,平面
,平面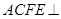 平面
平面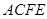 是矩形,
是矩形,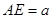 ,点
,点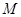 在线段
在线段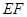 上.
上.
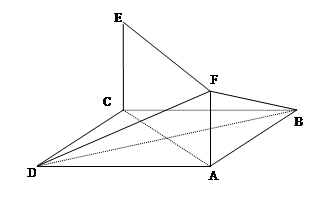
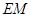 为何值时,
为何值时,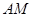 ∥平面
∥平面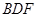 ?证明你的结论;
?证明你的结论;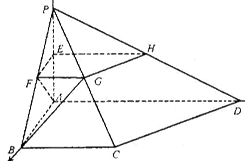
 ,
,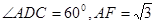
 粤公网安备 44130202000953号
粤公网安备 44130202000953号