（本小题12分）四棱锥P-ABCD中，PA⊥底面ABCD，AB∥CD，AD=CD=1，∠BAD=120°，PA=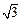
，∠ACB=90°。
（1）求证：BC⊥平面PAC；
（2）求二面角D-PC-A的大小的正切值；
（3）求点B到平面PCD的距离。
前
项和
.
中，角
的对边分别为
，已知
.
，求
的值.
中，
.
，求数列
的前
项和
.
成等比数列， 公比为
，求证：
.
都是锐角，且
，
，求
的值.推荐套卷
（本小题12分）四棱锥P-ABCD中，PA⊥底面ABCD，AB∥CD，AD=CD=1，∠BAD=120°，PA=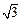，∠ACB=90°。
（1）求证：BC⊥平面PAC；
（2）求二面角D-PC-A的大小的正切值；
（3）求点B到平面PCD的距离。
粤公网安备 44130202000953号