（本小题共12分）已知函数
，
⑴若函数f(x)在区间（0，2）上递减，在[2，+∞）上递增，求a的值；
⑵在①的条件下是否存在实数m，使得函数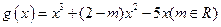
的图像与函数
的图像恰好有三个不同的交点，若存在，请求出实数m的取值范
围；若不存在，请说明理由。
相关试题
的度数；
的单调性；
、使得关于
的不等式
在(1，
)上恒成立，若存在，求出
，
，曲线
上的动点
满足
，直线
与曲线
．
，若
，求直线
的方程．
的底面
是菱形，
，其侧面展开图是边长为
的正方形。
、
分别是侧棱
、
上的动点，
．
；
在棱
，若
平面
，求
.
，求初三年级中女生比男生多的概率。推荐套卷
（本小题共12分）已知函数，
⑴若函数f(x)在区间（0，2）上递减，在[2，+∞）上递增，求a的值；
⑵在①的条件下是否存在实数m，使得函数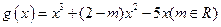的图像与函数的图像恰好有三个不同的交点，若存在，请求出实数m的取值范围；若不存在，请说明理由。
粤公网安备 44130202000953号