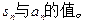设函数的定义域为（0，+∞），且对任意正实数x,y都有f(x·y)=f(x)+f(y)恒成立，已知f(2)=1且x>1时f(x)>0.
（1）求
；
（2）判断y=f(x)在(0,+ ∞)上的单调性；
（3）一个各项均为正数的数列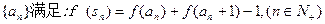
其中sn是数列
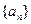的前n项和，求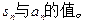
相关试题
在
与
时，都取得极值。
的值；
，求
的单调区间和极值；
都有
恒成立，求
的取值范围。
是定义在
上的奇函数,当
时，
.
.
中, a，b，c分别是A、B、C的对边，且
.
，
.
；
，求
的取值范围.
的面积为2，且
.
的值.相关知识点
推荐套卷
设函数的定义域为（0，+∞），且对任意正实数x,y都有f(x·y)=f(x)+f(y)恒成立，已知f(2)=1且x>1时f(x)>0.
（1）求；
（2）判断y=f(x)在(0,+ ∞)上的单调性；
（3）一个各项均为正数的数列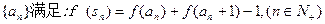其中sn是数列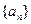的前n项和，求
粤公网安备 44130202000953号