如图,曲线
的方程为
.以原点为圆心,以
为半径的圆分别与曲线
和
轴的正半轴相交于点
与点
.直线
与
轴相交于点
.
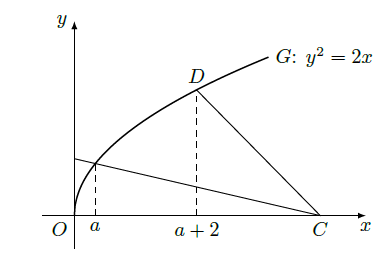
(Ⅰ)求点
的横坐标
与点
的横坐标
的关系式;
(Ⅱ)设曲线
上点
的横坐标为
,求证:直线
的斜率为定值.
推荐套卷
如图,曲线
的方程为
.以原点为圆心,以
为半径的圆分别与曲线
和
轴的正半轴相交于点
与点
.直线
与
轴相交于点
.

(Ⅰ)求点
的横坐标
与点
的横坐标
的关系式;
(Ⅱ)设曲线
上点
的横坐标为
,求证:直线
的斜率为定值.