（本小题满分14分）（注意：在试题卷上作答无效）
设数列
的前
项和为
，对一切
，点
都在函数
的图象上．
(Ⅰ)求
及数列的通项公式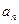
；
(Ⅱ) 将数列依次按1项、2项、3项、4项循环地分为（
），（
，
），（
，
，
），（
，
，
，
）；（
），（
，
），(
，
，
），（
，
，
，
）；（
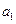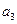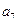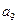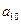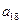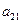），…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为
，求
的值；
（Ⅲ）令
（
），求证：
中，
，前n项的和
，求
.
中，
，且
，（n∈N*），求通项公式
.
是首项为1的正项数列，且
，（n∈N*），求数列的通项公式
.
中前n项的和
，求数列的通项公式
.
的前n项和为
，对于任意正整数n，都有等式：
成立，求
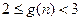
的通项an.推荐套卷
（本小题满分14分）（注意：在试题卷上作答无效）
设数列的前项和为，对一切，点都在函数 的图象上．
(Ⅰ)求及数列的通项公式；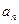
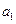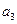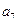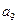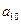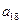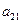(Ⅱ) 将数列依次按1项、2项、3项、4项循环地分为（），（，），（，，），（，，，）；（），（，），(，，），（，，，）；（），…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为，求的值；
（Ⅲ）令（），求证：
粤公网安备 44130202000953号