（本小题满分13分）（注意：在试题卷上作答无效）已知椭圆
和圆
：
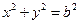，过椭圆上一点
引圆的两条切线，切点分别为
．
（Ⅰ）（ⅰ）若圆过椭圆的两个焦点，求椭圆的离心率
；
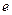（ⅱ）若椭圆上存在点，使得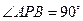
，求椭圆离心率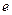的取值范围；
（Ⅱ）设直线
与
轴、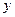
轴分别交于点
，
， 求证：
为定值．
推荐套卷
（本小题满分13分）（注意：在试题卷上作答无效）已知椭圆和圆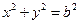：，过椭圆上一点引圆的两条切线，切点分别为．
（Ⅰ）（ⅰ）若圆过椭圆的两个焦点，求椭圆的离心率；
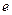（ⅱ）若椭圆上存在点，使得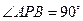，求椭圆离心率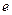的取值范围；
（Ⅱ）设直线与轴、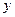轴分别交于点，， 求证：为定值．
粤公网安备 44130202000953号