(本小题满分12分)甲、乙两名射击运动员参加某项有奖射击活动(射击次数相同).已知两名运动员射击的环数都稳定在7,8,9,10环,他们射击成绩的条形图如下:
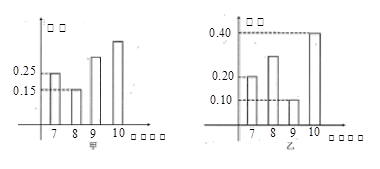
(Ⅰ)求乙运动员击中8环的概率,并求甲、乙同时击中9环以上(包括9环)的概率.
(Ⅱ)甲、乙两名运动员现在要同时射击4次,如果甲、乙同时击中9环以上(包括9环)3次时,可获得总奖金两万元;如果甲、乙同时击中9环以上(包括9环)4次时,可获得总奖金五万元,其他结果不予奖励.求甲、乙两名运动员可获得总奖金数的期望值.
(注:频率可近似看作概率)