(本小题满分14分)已知函数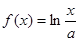 .
.
(1)若曲线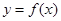 在
在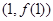 处的切线为
处的切线为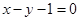 ,求
,求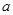 的值;
的值;
(2)设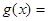
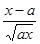 ,
,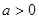 ,证明:当
,证明:当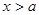 时,
时,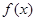 的图象始终在
的图象始终在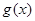 的图象的下方;
的图象的下方;
(3)当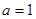 时,设
时,设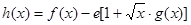 ,(
,(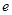 为自然对数的底数),
为自然对数的底数),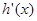 表示
表示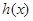 导函数,求证:对于曲线
导函数,求证:对于曲线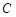 上的不同两点
上的不同两点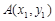 ,
,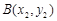 ,
,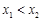 ,存在唯一的
,存在唯一的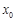
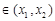 ,使直线
,使直线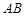 的斜率等于
的斜率等于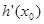 .
.
推荐套卷
(本小题满分14分)已知函数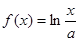 .
.
(1)若曲线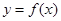 在
在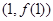 处的切线为
处的切线为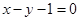 ,求
,求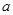 的值;
的值;
(2)设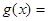
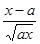 ,
,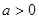 ,证明:当
,证明:当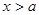 时,
时,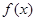 的图象始终在
的图象始终在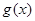 的图象的下方;
的图象的下方;
(3)当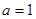 时,设
时,设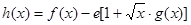 ,(
,(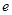 为自然对数的底数),
为自然对数的底数),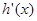 表示
表示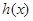 导函数,求证:对于曲线
导函数,求证:对于曲线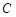 上的不同两点
上的不同两点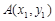 ,
,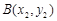 ,
,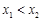 ,存在唯一的
,存在唯一的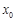
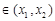 ,使直线
,使直线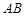 的斜率等于
的斜率等于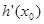 .
.