如图,在半径为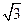 、圆心角为
、圆心角为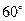 的扇形的弧上任取
的扇形的弧上任取 一点
一点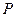 ,作扇
,作扇 形的内接矩形
形的内接矩形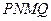 ,使点
,使点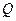 在
在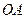 上,点
上,点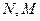 在
在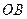 上,设矩形
上,设矩形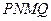 的面积为
的面积为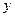 ,
,
(1)按下列要求写出函数的关系式:
① 设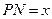 ,将
,将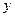 表示成
表示成 的函数关系式;
的函数关系式;
② 设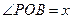 ,将
,将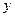 表
表 示成
示成 的函数关系式,
的函数关系式,
(2)请你选用(1)中的一个函数关系式,求出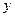 的最大值。
的最大值。
推荐套卷
如图,在半径为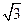 、圆心角为
、圆心角为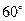 的扇形的弧上任取
的扇形的弧上任取 一点
一点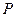 ,作扇
,作扇 形的内接矩形
形的内接矩形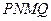 ,使点
,使点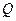 在
在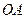 上,点
上,点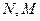 在
在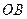 上,设矩形
上,设矩形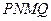 的面积为
的面积为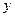 ,
,
(1)按下列要求写出函数的关系式:
① 设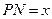 ,将
,将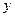 表示成
表示成 的函数关系式;
的函数关系式;
② 设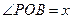 ,将
,将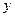 表
表 示成
示成 的函数关系式,
的函数关系式,
(2)请你选用(1)中的一个函数关系式,求出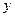 的最大值。
的最大值。