(本小题满分12分)
如图,四棱锥P—ABCD中, 底面ABCD,底面ABCD为正方形,|BC|=|PD|=3,E为PC的中点,点G在BC边上且
底面ABCD,底面ABCD为正方形,|BC|=|PD|=3,E为PC的中点,点G在BC边上且 。
。
(Ⅰ)三棱锥C—DEG的体积;
(Ⅱ)在AD边上是否存在点M,使得PA//平面MEG,
若存在,求 的值,若不存在,说明理由。
的值,若不存在,说明理由。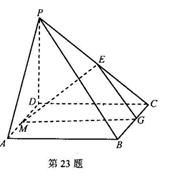
推荐套卷
(本小题满分12分)
如图,四棱锥P—ABCD中, 底面ABCD,底面ABCD为正方形,|BC|=|PD|=3,E为PC的中点,点G在BC边上且
底面ABCD,底面ABCD为正方形,|BC|=|PD|=3,E为PC的中点,点G在BC边上且 。
。
(Ⅰ)三棱锥C—DEG的体积;
(Ⅱ)在AD边上是否存在点M,使得PA//平面MEG,
若存在,求 的值,若不存在,说明理由。
的值,若不存在,说明理由。