在平面直角坐标系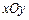
中，已知圆
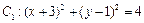和圆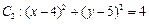
.
（1）若直线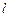
过点
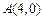，且被圆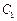
截得的弦长为
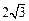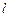，求直线的方程；
（2）设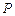
为平面上的点，满足：存在过点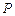的无穷多对互相垂直的直线
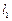和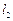
，它们分别与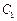圆和圆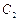
相交，且直线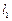被圆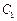截得的弦长与直线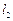被圆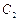截得的弦长相等，试求所有满足条件的点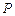的坐标.
C是椭圆上不同于A、B的点，求三角形ABC面积的最大值。
到焦点F2的距离也成等差数列。
推荐套卷
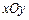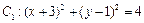在平面直角坐标系中，已知圆和圆.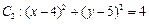
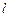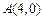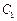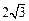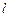（1）若直线过点，且被圆截得的弦长为，求直线的方程；
（2）设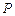为平面上的点，满足：存在过点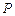的无穷多对互相垂直的直线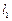和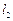，它们分别与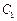圆和圆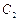相交，且直线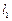被圆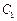截得的弦长与直线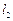被圆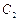截得的弦长相等，试求所有满足条件的点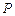的坐标.
粤公网安备 44130202000953号