（本小题满分12分）
已知函数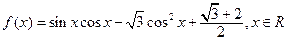
。
(1)求函数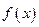
的最小正周期及函数取最小值时自变量
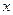的集合；
(2)确定函数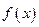的单调递增区间；
(3)若函数y=sin2x的图象向右平移m个单位(|m|<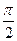
)，向上平移n个单位后得到函数y=f(x)的图象，求实数m、n的值。
，
，
是同一平面内的三个向量，其中
.
，且
，求
，且
与
垂直，求
.
（
，
）为偶函数，其图象上相邻的两个最高点之间的距离为
．
的解析式；（2）若
，
，求
的值．
，求函数在区间
上的单调增区间；
.
，
.
的最小正周期；（2）求
，求
的值.
，
，求
的值.推荐套卷
（本小题满分12分）
已知函数。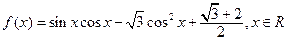
(1)求函数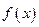的最小正周期及函数取最小值时自变量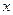的集合；
(2)确定函数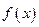的单调递增区间；
(3)若函数y=sin2x的图象向右平移m个单位(|m|<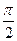)，向上平移n个单位后得到函数y=f(x)的图象，求实数m、n的值。
粤公网安备 44130202000953号