(本小题满分12分) 已知函数f (x) = ax2 + 2ln(1-x),其中a∈R.
(1)是否存在实数a,使得f (x)在x = 处取极值?若存在,求出a的值,若不存在,说明理由;
处取极值?若存在,求出a的值,若不存在,说明理由;
(2)若f (x)在[-1,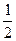 ]上是减函数,求实数a的取值范围.
]上是减函数,求实数a的取值范围.
推荐套卷
(本小题满分12分) 已知函数f (x) = ax2 + 2ln(1-x),其中a∈R.
(1)是否存在实数a,使得f (x)在x = 处取极值?若存在,求出a的值,若不存在,说明理由;
处取极值?若存在,求出a的值,若不存在,说明理由;
(2)若f (x)在[-1,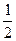 ]上是减函数,求实数a的取值范围.
]上是减函数,求实数a的取值范围.