（本小题满分12分）
某市地铁全线共有四个车站，甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对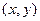
表示“甲在
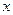号车站下车，乙在
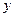号车站下车”．
（1）用有序实数对把甲、乙两人下车的所有可能的结果列举出来；
（2）求甲、乙两人同在第3号车站下车的概率；
（3）求甲、乙两人在不同的车站下车的概率．
满足关系
，试比较
与
的大小。
都是实数，求证
中，
,
,如果向该矩形内随机投一点
，
与△
面积都不小于
的概率
的全
项和为
.若
，求数列的公比
.推荐套卷
（本小题满分12分）
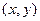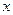某市地铁全线共有四个车站，甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对表示“甲在号车站下车，乙在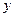号车站下车”．
（1）用有序实数对把甲、乙两人下车的所有可能的结果列举出来；
（2）求甲、乙两人同在第3号车站下车的概率；
（3）求甲、乙两人在不同的车站下车的概率．
粤公网安备 44130202000953号