（本小题满分12分）已知二阶矩阵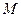
有特征值
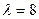及对应的一个特征向量
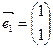，并且矩阵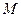对应的变换将点（-1，2）变换成（-2，4）.
（1）求矩阵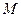
（2）求矩阵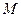的另一个特征值及对应的一个特征向量
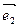的坐标之间关系
（3）求直线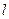
：
在矩阵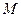的作用下的直线
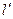的方程
相关试题
的定义域;
的值．
在定义域
上是减函数且为奇函数，若
求实数
的取值范围．
是R上的奇函数，且当x<0时，函数的解析式为
求函数
；
，
．
，求
的取值范围；
，求推荐套卷
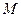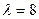（本小题满分12分）已知二阶矩阵有特征值及对应的一个特征向量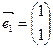，并且矩阵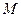对应的变换将点（-1，2）变换成（-2，4）.
（1）求矩阵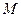
（2）求矩阵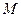的另一个特征值及对应的一个特征向量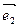的坐标之间关系
（3）求直线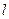：在矩阵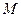的作用下的直线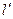的方程
粤公网安备 44130202000953号