设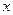 轴、
轴、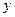 轴正方向上的单位向量分别是
轴正方向上的单位向量分别是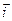 、
、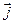 ,坐标平面上点
,坐标平面上点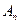 、
、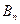
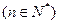 分别满足下列两个条件:
分别满足下列两个条件:
① 且
且
 ;
;
②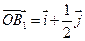 且
且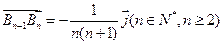 .(其中
.(其中 为坐标原点)
为坐标原点)
(I)求向量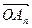 及向量
及向量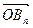 的坐标;
的坐标;
(II)设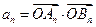 ,求
,求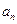 的通项公式并求
的通项公式并求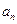 的最小值;
的最小值;
(III)对于(Ⅱ)中的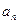 ,设数列
,设数列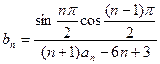 ,
, 为
为 的前n项和,证明:对所有
的前n项和,证明:对所有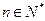 都有
都有 .
.
推荐套卷
设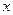 轴、
轴、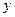 轴正方向上的单位向量分别是
轴正方向上的单位向量分别是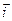 、
、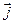 ,坐标平面上点
,坐标平面上点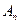 、
、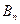
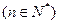 分别满足下列两个条件:
分别满足下列两个条件:
① 且
且
 ;
;
②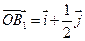 且
且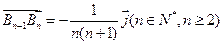 .(其中
.(其中 为坐标原点)
为坐标原点)
(I)求向量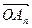 及向量
及向量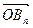 的坐标;
的坐标;
(II)设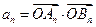 ,求
,求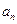 的通项公式并求
的通项公式并求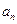 的最小值;
的最小值;
(III)对于(Ⅱ)中的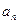 ,设数列
,设数列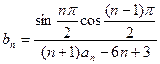 ,
, 为
为 的前n项和,证明:对所有
的前n项和,证明:对所有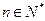 都有
都有 .
.