某班主任对班级22名学生进行了作业量多少的调查，数据如下表：在喜欢玩电脑游戏的12中，有10人认为作业多，2人认为作业不多；在不喜欢玩电脑游戏的10人中，有3人认为作业多，7人认为作业不多。求：（1）根据以上数据建立一个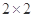
列联表；（2）试问喜欢电脑游戏与认为作业多少是否有关系？
的定义域.
－α)＝
，求cos(
π＋α)＋sin2(α－
，求f(α)的值；
推荐套卷
某班主任对班级22名学生进行了作业量多少的调查，数据如下表：在喜欢玩电脑游戏的12中，有10人认为作业多，2人认为作业不多；在不喜欢玩电脑游戏的10人中，有3人认为作业多，7人认为作业不多。求：（1）根据以上数据建立一个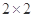列联表；（2）试问喜欢电脑游戏与认为作业多少是否有关系？
粤公网安备 44130202000953号