（本题16分）如图,某大风车的半径为2米,每12秒沿逆时针方向旋转一周,它的最底点
离地面1米,风车圆周上一点A从最底点开始,运动t秒后与地面距离为h米，
(1)求函数h=f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点)；
(2) A从最底点开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?
相关试题
，计算：
（2）
，
。
，
；（2）若
为单位向量，求
表示
导函数。
为奇数时，设
，数列
的前
项和为
，证明不等式
对一切正整数
与
的大小.
平面
，
平面
，
为
的中点．
平面
；
平面
；
和平面
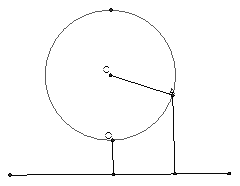
推荐套卷
（本题16分）如图,某大风车的半径为2米,每12秒沿逆时针方向旋转一周,它的最底点离地面1米,风车圆周上一点A从最底点开始,运动t秒后与地面距离为h米，
(1)求函数h=f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点)；
(2) A从最底点开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?
粤公网安备 44130202000953号