某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如下图所示.
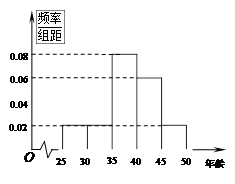
(Ⅰ)下表是年龄的频数分布表,求正整数a,b的值;
区间
|
[25,30)
|
[30,35)
|
[35,40)
|
[40,45)
|
[45,50]
|
人数
|
50
|
50
|

|
150
|

|
(Ⅱ) 现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(III)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.