（理科做）
甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.6，本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响．令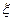
为本场比赛的局数．求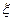的概率分布和数学期望．（精确到0.0001）
相关试题
的前
项和为
，且
．
，数列
的前
，若不等式
对任意
恒成立，求实数
的取值范围．
．
的零点；
在
上有解，求实数
的取值范围．
首项
，公差为
，且数列
是公比为4的等比数列，
及前
项和
； 
的前
．
函数
解析式； 
的单调递减区间；
上的图像．（要求列表、描点、连线）
．
；
，且
是第二象限角，求
的值．推荐套卷
（理科做）
甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.6，本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响．令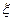为本场比赛的局数．求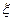的概率分布和数学期望．（精确到0.0001）
粤公网安备 44130202000953号