设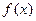 是定义在实数
是定义在实数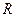 上的函数,
上的函数,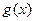 是定义在正整数
是定义在正整数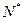 上的函数,同时满足下列条件:
上的函数,同时满足下列条件:
(1)任意 ,有
,有 ,当
,当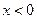 时,
时,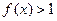 且
且 ;
;
(2)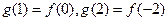 ;
;
(3)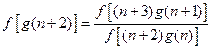 ,
,
试求:(1)证明:任意 ,
,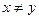 ,都有
,都有 ;
;
(2)是否存在正整数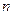 ,使得
,使得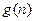 是25的倍数,若存在,求出所有自然数
是25的倍数,若存在,求出所有自然数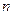 ;若不存在说明理由.(阶乘定义:
;若不存在说明理由.(阶乘定义: )
)
推荐套卷
设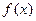 是定义在实数
是定义在实数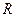 上的函数,
上的函数,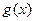 是定义在正整数
是定义在正整数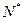 上的函数,同时满足下列条件:
上的函数,同时满足下列条件:
(1)任意 ,有
,有 ,当
,当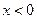 时,
时,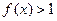 且
且 ;
;
(2)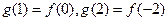 ;
;
(3)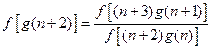 ,
,
试求:(1)证明:任意 ,
,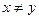 ,都有
,都有 ;
;
(2)是否存在正整数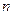 ,使得
,使得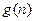 是25的倍数,若存在,求出所有自然数
是25的倍数,若存在,求出所有自然数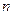 ;若不存在说明理由.(阶乘定义:
;若不存在说明理由.(阶乘定义: )
)