(本小题满分14分)
某公司计划2010年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过180000元,甲、乙两个电视台的广告收费标准分别为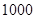 元/分钟和
元/分钟和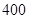 元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为3000元和2000元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少元?
元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为3000元和2000元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少元?
推荐套卷
(本小题满分14分)
某公司计划2010年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过180000元,甲、乙两个电视台的广告收费标准分别为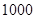 元/分钟和
元/分钟和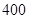 元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为3000元和2000元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少元?
元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为3000元和2000元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少元?