（本小题满分12分）
现有甲、乙两个口袋，甲袋装有2个红球和2个白球，乙袋装有2个红球和n个白球，某人从甲、乙两个口袋中等可能性地各取2个球．
（1）若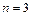
，求取到的4个球全是红球的概率；
（2）若取到的4个球中至少有2个红球的概率为
，求n的值．
相关试题
平面
，
、
是夹在两条平行平面间的两条线段，
、
在
内，
、
在
、
分别在
．求证：
．
，直线
与
分别交
，
，
于点
，
，
和
，
，
，求证
．
中，
，
分别是
，
的中点．
求证：
的两个焦点为
，点
在椭圆
上，
，
的取值范围，使得椭圆上有两个不同的点关于直线
对称．
中，
分别是三个内角
的对边．若
，
，
的余弦值；
．相关知识点
推荐套卷
（本小题满分12分）
现有甲、乙两个口袋，甲袋装有2个红球和2个白球，乙袋装有2个红球和n个白球，某人从甲、乙两个口袋中等可能性地各取2个球．
（1）若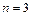，求取到的4个球全是红球的概率；
（2）若取到的4个球中至少有2个红球的概率为，求n的值．
粤公网安备 44130202000953号