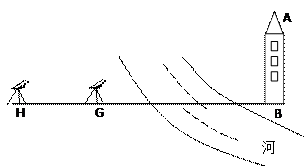（本小题满分12分）
如图，在某平原地区一条河的彼岸有一建筑物，现在需要测量其高度AB.由于雨季河宽水急不能涉水，只能在此岸测量.现有的测量器材只有测角仪和皮尺.现在选定了一条水平基线HG,使得H、G、B三点在同一条直线上.请你设计一种测量方法测出建筑物的高度，并说明理由.（测角仪的高为h）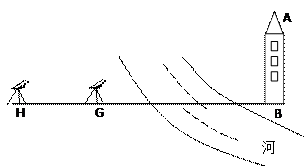
相关试题
，其中
．
时，证明
；
在区间
，
内各有一个根，求
的取值范围；
的首项
，前
项和
，
，求
，并判断
中，
，
（
），
是数列
；
满足
（
项和
．
的三个内角
成等差数列，它们的对边分别为
，且满足
，
．
；
．
．
的最小正周期；
，且
，求
．
，
，
，
．
与
的夹角；
，求实数
的值．推荐套卷
（本小题满分12分）
如图，在某平原地区一条河的彼岸有一建筑物，现在需要测量其高度AB.由于雨季河宽水急不能涉水，只能在此岸测量.现有的测量器材只有测角仪和皮尺.现在选定了一条水平基线HG,使得H、G、B三点在同一条直线上.请你设计一种测量方法测出建筑物的高度，并说明理由.（测角仪的高为h）
粤公网安备 44130202000953号