设椭圆 的两个焦点是
的两个焦点是 ,且椭圆上存在点M,使
,且椭圆上存在点M,使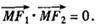
(1)求实数m的取值范围;
(2)若直线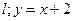 与椭圆存在一个公共点E,使得|EF
与椭圆存在一个公共点E,使得|EF |+|EF
|+|EF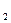 |取得最小值,求此最小值及此时椭圆的方程;
|取得最小值,求此最小值及此时椭圆的方程;
(3)在条件(2)下的椭圆方程,是否存在斜率为 的直线
的直线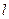 ,与椭圆交于不同的两A,B,满足
,与椭圆交于不同的两A,B,满足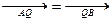 ,且使得过点
,且使得过点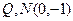 两点的直线NQ满足
两点的直线NQ满足 =0?若存在,求出k的取值范围;若不存在,说明理由
=0?若存在,求出k的取值范围;若不存在,说明理由
推荐套卷
设椭圆 的两个焦点是
的两个焦点是 ,且椭圆上存在点M,使
,且椭圆上存在点M,使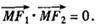
(1)求实数m的取值范围;
(2)若直线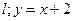 与椭圆存在一个公共点E,使得|EF
与椭圆存在一个公共点E,使得|EF |+|EF
|+|EF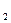 |取得最小值,求此最小值及此时椭圆的方程;
|取得最小值,求此最小值及此时椭圆的方程;
(3)在条件(2)下的椭圆方程,是否存在斜率为 的直线
的直线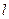 ,与椭圆交于不同的两A,B,满足
,与椭圆交于不同的两A,B,满足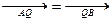 ,且使得过点
,且使得过点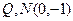 两点的直线NQ满足
两点的直线NQ满足 =0?若存在,求出k的取值范围;若不存在,说明理由
=0?若存在,求出k的取值范围;若不存在,说明理由