已知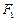 ,
,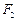 分别是双曲线
分别是双曲线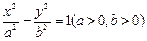 的左右焦点,以坐标原点
的左右焦点,以坐标原点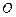 为圆心,以双曲线的半焦距
为圆心,以双曲线的半焦距 为半径的圆与双曲线在第一象限的交点为
为半径的圆与双曲线在第一象限的交点为 ,与
,与 轴正半轴的交点为
轴正半轴的交点为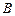 ,点
,点 在
在 轴上的射影为
轴上的射影为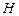 ,且
,且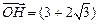
 .
.
⑴求双曲线的离心率;
⑵若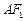 交双曲线于点
交双曲线于点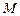 ,且
,且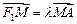 ,求
,求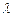 .
.
相关知识点
推荐套卷
已知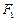 ,
,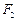 分别是双曲线
分别是双曲线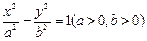 的左右焦点,以坐标原点
的左右焦点,以坐标原点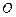 为圆心,以双曲线的半焦距
为圆心,以双曲线的半焦距 为半径的圆与双曲线在第一象限的交点为
为半径的圆与双曲线在第一象限的交点为 ,与
,与 轴正半轴的交点为
轴正半轴的交点为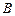 ,点
,点 在
在 轴上的射影为
轴上的射影为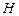 ,且
,且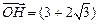
 .
.
⑴求双曲线的离心率;
⑵若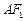 交双曲线于点
交双曲线于点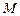 ,且
,且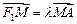 ,求
,求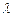 .
.