（本小题满分12分）
已知函数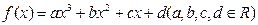
，且函数
的图象关于原点
对称，其图象在x=3处的切线方程为
（1）求的解析式；
（2）是否存在区间[m，n]，使得函数
的定义域和值域均为[m，n]，且其解析式为 的解析式？若存在，求出这样一个区间[m，n]；若不存在，则说明理由.
是等差数列，数列
的前n项和
，若
，
，（1）求数列
．
，
时，求
的值．
在
上的最大值．
．
分成两段弧，其中劣弧最短时，求直线l的方程。推荐套卷
（本小题满分12分）
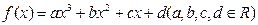已知函数，且函数的图象关于原点
对称，其图象在x=3处的切线方程为
（1）求的解析式；
（2）是否存在区间[m，n]，使得函数的定义域和值域均为[m，n]，且其解析式为 的解析式？若存在，求出这样一个区间[m，n]；若不存在，则说明理由.
粤公网安备 44130202000953号