（1）当你手握直角三角板，其斜边保持不动，将其直角顶点提起一点，则直角在平面内的正投影是锐角、直角 还是钝角？
（2）根据第（1）题，你能猜想某个角在一个平面内的正投影一定大于这个角吗？如果正确，请证明；如果错误，则利用下列三角形举出反例：△ABC中，
，
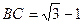，以∠BAC为例。
，
，在
轴上求点
，使
．
与已知圆
的交点，且在两坐标轴上的四个截距之和为
的圆的方程．
表示一个圆．
的取值范围；
的取值范围．
，在坐标轴上求一点
，使直线
的倾斜角为
．
在
轴上的截距为
，直线
的两点的线段长为
，求直线推荐套卷
（1）当你手握直角三角板，其斜边保持不动，将其直角顶点提起一点，则直角在平面内的正投影是锐角、直角 还是钝角？
（2）根据第（1）题，你能猜想某个角在一个平面内的正投影一定大于这个角吗？如果正确，请证明；如果错误，则利用下列三角形举出反例：△ABC中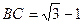，，，以∠BAC为例。
粤公网安备 44130202000953号