.(本小题满分12分)一位客人去北京旅游,他游览长城、故宫、鸟巢这三个景点的概率分别为0.9、0.8、0.8,且他是否游览哪个景点互不影响.设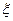 表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
(1)求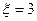 时的概率;
时的概率;
(2)记“函数 在区间
在区间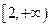 上是增函数”为事件A,求事件A的概率.
上是增函数”为事件A,求事件A的概率.
相关知识点
推荐套卷
.(本小题满分12分)一位客人去北京旅游,他游览长城、故宫、鸟巢这三个景点的概率分别为0.9、0.8、0.8,且他是否游览哪个景点互不影响.设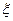 表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
(1)求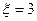 时的概率;
时的概率;
(2)记“函数 在区间
在区间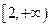 上是增函数”为事件A,求事件A的概率.
上是增函数”为事件A,求事件A的概率.