为了对某课题进行研究,用分层抽样方法从三所高校
的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
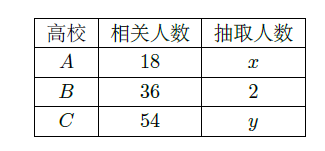
(I)求
;
(II)若从高校
抽取的人中选2人作专题发言,求这二人都来自高校
的概率。
推荐套卷
为了对某课题进行研究,用分层抽样方法从三所高校
的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)

(I)求
;
(II)若从高校
抽取的人中选2人作专题发言,求这二人都来自高校
的概率。