在平面直角坐标系 中,如图,已知椭圆 的左右顶点为 ,右顶点为 ,设过点 的直线 与椭圆分别交于点 , ,其中 ,
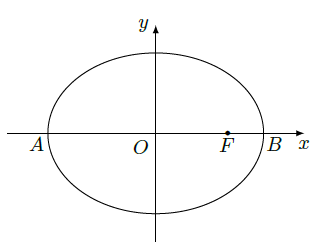
①设动点
满足
,求点
的轨迹
②设
,求点
的坐标
③设
,求证:直线
必过
轴上的一定点(其坐标与
无关)
推荐套卷
在平面直角坐标系 中,如图,已知椭圆 的左右顶点为 ,右顶点为 ,设过点 的直线 与椭圆分别交于点 , ,其中 ,

①设动点
满足
,求点
的轨迹
②设
,求点
的坐标
③设
,求证:直线
必过
轴上的一定点(其坐标与
无关)