(本小题满分13分)已知点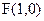 ,直线
,直线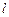 :
: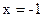 ,
,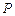 为平面上的动点,过点
为平面上的动点,过点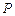 作直线
作直线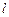 的垂线,垂足为
的垂线,垂足为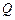 ,且
,且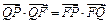 .(1)求动点
.(1)求动点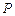 的
的 轨迹
轨迹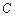 的方程;
的方程;
(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k1、k2满足 ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。
相关知识点
推荐套卷
(本小题满分13分)已知点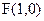 ,直线
,直线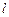 :
: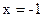 ,
,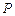 为平面上的动点,过点
为平面上的动点,过点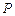 作直线
作直线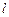 的垂线,垂足为
的垂线,垂足为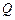 ,且
,且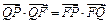 .(1)求动点
.(1)求动点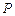 的
的 轨迹
轨迹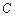 的方程;
的方程;
(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k1、k2满足 ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。