已知函数 .
.
(Ⅰ)求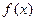 的极值;
的极值;
(II)判断y=f(x)的图像是否是中心对称图形,若是求出对称中心并证明,否则说明理由;
(III)设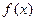 的定义域为
的定义域为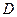 ,是否存在
,是否存在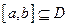 .当
.当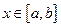 时,
时,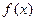 的取值范围是
的取值范围是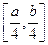 ?若存在,求实数
?若存在,求实数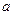 、
、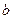 的值;若不存在,说明理由
的值;若不存在,说明理由
推荐套卷
已知函数 .
.
(Ⅰ)求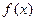 的极值;
的极值;
(II)判断y=f(x)的图像是否是中心对称图形,若是求出对称中心并证明,否则说明理由;
(III)设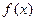 的定义域为
的定义域为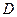 ,是否存在
,是否存在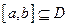 .当
.当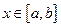 时,
时,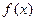 的取值范围是
的取值范围是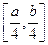 ?若存在,求实数
?若存在,求实数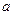 、
、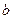 的值;若不存在,说明理由
的值;若不存在,说明理由