(本小题满分12分)
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤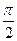 )的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若
)的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若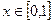 ,求函数y=2sin(πx+φ)的最值,及取得最值时
,求函数y=2sin(πx+φ)的最值,及取得最值时 的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求
的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求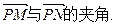 的余弦值。
的余弦值。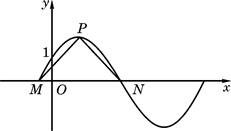
推荐套卷
(本小题满分12分)
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤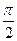 )的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若
)的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若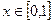 ,求函数y=2sin(πx+φ)的最值,及取得最值时
,求函数y=2sin(πx+φ)的最值,及取得最值时 的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求
的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求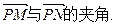 的余弦值。
的余弦值。