(本小题满分12分)如图，在三棱锥A－BCD中，侧面ABD、 ACD是全等的直角三角形，AD是公共的斜边，且AD＝
，BD＝CD＝1，另一个侧面是正三角形.
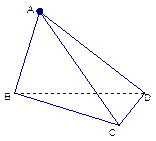
（1） 求证：AD^BC;
（2） 求二面角B－AC－D的大小;
（3） 在直线AC上是否存在一点E，使ED与面BCD成30°角？若存在，确定E的位置；若不存在，说明理由
相关试题
+ sin2α﹣3sinα•cosα的值。
，1），求
的值
的两根为sinθ和cosθ：
的值；
；
}满足
。
}是等比数列。
。推荐套卷
(本小题满分12分)如图，在三棱锥A－BCD中，侧面ABD、 ACD是全等的直角三角形，AD是公共的斜边，且AD＝，BD＝CD＝1，另一个侧面是正三角形.
（1） 求证：AD^BC;
（2） 求二面角B－AC－D的大小;
（3） 在直线AC上是否存在一点E，使ED与面BCD成30°角？若存在，确定E的位置；若不存在，说明理由
粤公网安备 44130202000953号