(本小题满分14分)
为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:
分组
|
频数累计
|
频数
|
频率
|
[10.75,10.85)
|
6
|
6
|
0.06
|
[10.85,10.95)
|
15
|
9
|
0.09
|
[10.95,11.05)
|
30
|
15
|
0.15
|
[11.05,11.15)
|
48
|
18
|
0.18
|
[11.15,11.25)
|
▲
|
▲
|
▲
|
[11.25,11.35)
|
84
|
12
|
0.12
|
[11.35,11.45)
|
92
|
8
|
0.08
|
[11.45,11.55)
|
98
|
6
|
0.06
|
[11.55,11.65)
|
100
|
2
|
0.02
|
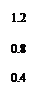
(Ⅰ)完成频率分布表;
(Ⅱ)画出频率分布直方图;
(Ⅲ)据上述图表,估计产品直径落在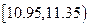 范围内的可能性是百分之几?
范围内的可能性是百分之几?